Part IV

In genetics, canalization is the ability of a genotype to produce the same phenotype regardless of the environmental setting. In an evolutionary context, canalization (often spelled canalisation) is a manifestation of historical contingency. Once a successful genotype arises it tends to persist, and other evolutionary pathways are closed off. The evolutionary trajectory is in some senses confined to a "channel," the metaphor that produced the term canalization. The term, originally due to biologist C.H. Waddington, has since been used by others in a broader sense to refer to historical development phenomena whereby once a particular path is "chosen" there is an element of lock-in (the quotes are not only because Earth surface systems (ESS) lack intentionality, but also because the selection may be due to random chance or be highly sensitive to minuscule variations).

Canalization also has a more literal meaning, of course, associated with the construction of canals and channelization of rivers. This one is in the Netherlands.

Positive feedbacks may play an important role. To use an example where the channelization metaphor is literally applicable, whether a channel forms here or a few meters away may be influenced (via dynamical instability) by such tiny variations as to be pseudorandom. Once formed, however, the new channel is a more efficient flow path, and those flows help maintain it, and scour may enlarge it. The formation of the channel was not preordained or deterministically predictable with respect to its precise location, but once established it closes off some previously possible channel locations and strongly influences down-gradient channel locations.

Irreversibility can also play a role. Once a portion of a hillslope fails, for example, the slumped material is not going to return to its original location. The mass movement, and the associated rearrangement of slope morphology influences future slope processes, making some pathways and outcomes more, and others less, likely. That is, slope development is to some extent canalized.

Can the effects of canalization be treated analytically? In mathematical or statistical principle, yes--but I have figured no way to do it in practice.

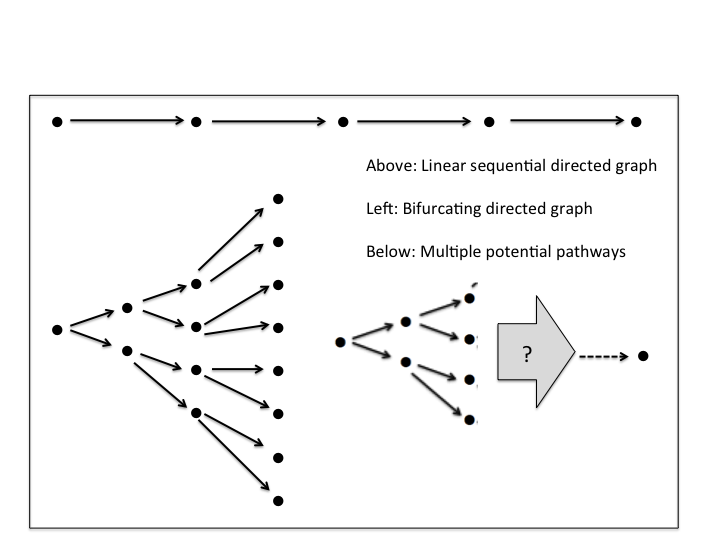
From the perspective of predicting future evolution, or identifying possible alternative developmental pathways from a (known or hypothetical) past starting point, multiple possibilities at each stage or iteration must be considered. Speciation, for instance, depends on random genetic variability and is non-deterministic. The direction of hydrological flow paths depends on the "choice" of alternative routes, which could be deterministically predicted only with essentially perfect, detailed knowledge of both the flux and the environment. For the simplest case of two possibilities at each iteration, there are therefore 2^^q possible outcomes at the q^th stage. Therefore, for example, a water flow path from a single location could occupy any of 32 different locations after q = 5 cases of a binary selection of alternative flow paths. This can be represented as a directed graph of the binary tree type. Assuming equal probability at each bifurcation, the probability of any single particular outcome at q iterations is 1/2^^q = 0.5^^q.

Of course, as development proceeds some of the initial possibilities are closed off. Considering the bifurcation situation, at each iteration or junction, the number of possibilities is cut in half. A sequence of 10 bifurcations, for instance, has 1024 possible outcomes. After the first split, however, half of those are no longer possible, and so on at each bifurcation. Denoting the total number of iterations as q_max, the number of possibilities after q (< q_max) stages is 2^^{(qmax - q)}.

Assuming at least two possibilities at each evolutionary or developmental crossroads, this suggests that at each stage or iteration of ESS evolution, the number of possibilities that existed before that stage is reduced by at least half.

Posted 27 July 2017

Part I              Part II             Part III

2 + 2 = 4.

That is non-contingent. Adding two and two gives the same result no matter who does it, how they do it, where they do it, or when. The same goes for expressions such as 2 + X = 4, or 27/X = 4, etc.

This four-play is a metaphor for the deterministic, Laplacian, non-contingent ideal of science, where the right tools and sufficient information always give the same, correct result under any circumstances.

But a better metaphor for the actual practice of geosciences and other historical, field-based sciences, is that you find, or observe (evidence of) a four. Mathematically, of course, there are an infinite number of numerical operations that could produce a four. Even if you know that the four arose from, say, subtraction or exponentiation, the possibilities are still infinite.

Sometimes we can discover clues or information that allow us to construct something like an algebraic expression and make the problem more deterministic. More often, however, we are faced with constraining, somehow, the infinite possibilities.

For a simple but realistic example, think of stream discharge (Q), which (using the Chezy Equation) is given by

where w and d are width and mean depth, C is the Chezy coefficient (which combines some physical constants with a roughness or friction factor), R is hydraulic radius (cross-sectional area divided by wetted perimeter), and S is the energy grade slope.

You have an observation of Q, and you want to know the properties of the flow that produced it (these kinds of problems come up in paleohydrologic reconstruction as well as in studies of flow hydraulics). Even if you assume, as is often the case, with some validity, that R ≈ d, you have five variables to consider. In terms of the arithmetic, there are an infinite combination of values of w, d, C, and S that could produce a given Q. But you can constrain the infinite possibilities; you have to if you hope to make a decent stab at the problem.

Multiple active & paleochannels, lower Neches River, Texas (Fig. 7 from this).

Presumably you have some idea of the dimensions of the channel. Based on the banktop width you can (assuming the flow was not an overbank flood) eliminate values of w higher than this, and perhaps also identify implausibly low widths. Similarly, you may be able to constrain plausible depths based on local base levels, the topographic setting, and geotechnical constraints on bank heights in a given material. S is not exactly the same as channel bed slope, but is pretty close in some cases, and you can often identify a range of possible energy grade slope values.

Of course even if you know, for instance, that width had to be somewhere between 5 and 15 m, and depth <5 m, there are still an infinite number of values between 5 and 15 or 0 and 5. Commonsensical considerations can make this finite, for example by limiting the values to 1, 2, or 3 decimal places (who measures in the field to the nearest millimeter, anyway?).  But you still often have multiple, sometimes many, possibilities.

Mathematicians and philosophers have long pondered, and continue to debate, whether infinity is a concept with real physical meaning, or simply a useful mathematical abstraction. Whether or not there are truly unlimited numbers of possible stream channel geometries, vegetation compositions, or whatever, there are clearly in our business some cases where the number of possibilities are essentially infinite, in the sense of having no known upper or lower limit, or far more possibilities than we can deal with--or that could occur. Imagine some type of bifurcating system of 60 iterations. As the number of seconds elapsed since the Big Bang is about 2^59, they'd have to occur at a frequency of >1/sec, starting at the beginning, to realize all the possibilities.

In terms of arithmetic, ∞ = ∞. But not all infinities are equal. For example there are an infinite number of odd integers, the set of odd and even integers is also infinite, and so is the set of all real numbers. All those are equal to ∞, but each set mentioned is successively larger.

Yadier Molina, an example of the only type of Cardinal that I understand.

The cardinality of set is the number of elements in that set, so even though ∞ = ∞, the cardinality of the infinite sets mentioned above differs. There exists a set of rules for an algebra of cardinal numbers, or combinations of cardinalities and finite numbers. I messed with this some in homes it would help me come to terms with some of the ESS evolution contingencies that vex me. But I did not find it helpful, perhaps because I do not understand it very well.

Posted: 24 July 2017

The “perfect storm” metaphor describes the improbable coincidence of several different forces or factors to produce an unusual outcome. The perfect landscape refers to the result of the combined, interacting effects of multiple environmental controls and forcings to produce an outcome that is highly improbable, in the sense of the likelihood of duplication at any other place or time (Phillips, 2007a). Geomorphic and other Earth surface systems (ESS) have multiple environmental controls and forcings, and multiple degrees of freedom in responding to them. This alone allows for many possible landscapes and system states. Further, some controls are contingent, and these contingencies are specific to time and place. Dynamical instability in many ESS creates and enhances some of this contingency by causing the effects of minor initial variations and small disturbances to persist and grow over time. The joint probability of any particular set of global controls (laws or non-contingent generalizations) is low, as the individual probabilities are <1. The probability of any set of local, contingent controls is even lower.

Rabbit bioturbation in South Australia. This is an example of a perfect landscape—because they all are.

Hence, the probability of existence of any ESS state at a particular place and time is negligibly small: all landscapes are perfect. The perfect landscape perspective leads toward a worldview that landforms and landscapes are circumstantial, contingent results of deterministic laws operating in a specific environmental context, such that multiple outcomes are possible.

The laws, place, history framework (LPH) is an extension of the perfect landscape concept, mainly as a pedagogical device, but it also has some analytical utility (Phillips, 2017). The laws correspond the “global” factors in the perfect landscape framework, and are the non-contingent generalizations that apply to any ESS of a given type. The “local,” contingent factors are in the LPH split into geographically and historically contingent aspects.

Expanding the mathematic representation of the perfect landscape paper to the LPH framework, we come up with an expression for the probability of existence of any given ESS state:

This indicates that p(S) is a function of the product of the probabilities of n applicable laws, m geographically contingent place factors or environmental controls, and q historically contingent events or episodes. As all p(L) < 1, and p(P), p(H) < 1, and often << 1, this shows the negligibly small probabilities of any given ESS state, at least if considered in significant detail. It also illustrates the related point that the more factors (L, P, or H) considered, the more specific and idiosyncratic the representation will be.

A perfect gully & slope failure: the Tarndale Slip near Gisborne, New Zealand.

Perfection and the LPH framework are pedagogically useful for communicating ideas about contingency in ESS evolution, and provide a formal way of expressing it. The equation above does rigorously demonstrate some key points, but does not (at least thus far) provide a tool for addressing the issues raised in Part I; i.e. reconciling the historical inevitability of what did happen with the many possible evolutionary trajectories that exist.

The language of perfection (with props to Sebastian Junger, whose book launched the perfect storm metaphor) was quite deliberately chosen. This relates to the “learned to love contingency” part of the title. While perfection poses clear scientific challenges, it also leads to the magnificent, often delightful, variety of the world around us.

Previous writings on these topics:

Phillips, J.D.  2006.  Evolutionary geomorphology: thresholds and nonlinearity in landform response to environmental change. Hydrology and Earth System Sciences 10: 731-742.

Phillips, J.D.  2007a.  The perfect landscape.  Geomorphology 84: 159-169.

Phillips, J.D., 2007b.  Perfection and complexity in the lower Brazos River.  Geomorphology 91: 364-377.

Phillips, J.D., 2015. Badass geomorphology. Earth Surface Processes & Landforms 40, 22-33.

Philliips, J.D., 2017. Laws, place, history and the interpretation of landforms. Earth Surface Processes & Landforms 42: 347-354.

Next: Infinite constraints

Posted: 21 July 2017

Part I

My first, and abiding, interest in complex nonlinear dynamics arose in an effort to explain the extensive spatial variability in geomorphic and pedologic phenomena often found within short distances and small areas, in the absence of measurable variations in explanatory factors. Dynamical instability and chaos, whereby minor variations in initial conditions or effects of small, local disturbances become exaggerated over time, can explain this phenomenon. We have had considerable success over the past 25 or 30 years in this regard.

Soil profiles exposed on the Neuse River estuary shoreline, Croatan, N.C. Complex local spatial variability--despite uniform parent material--is evident. Dynamical instability and chaos in pedogenesis of the these soils was demonstrated nearly 25 years ago.

Deterministic chaos (in most cases directly equivalent to dynamical instability) is also, however, at least a decent metaphor for historical contingency in the evolution of Earth surface systems (ESS).  In a chaotic system, multiple trajectories and outcomes are possible from a single starting point. Same for historically contingency, path dependent evolution. In a chaotic system complex, complicated, pseudo-random patterns can be generated by relatively simple deterministic dynamics. There is also simplicity embedded within the complexity of historically contingent development in the sense that only one sequence of events or changes did occur, out of the many that could have occurred. The two phenomena are also similar in that both are guided and constrained by general laws.

Dynamical instability and chaos are also an important form of historical contingency in ESS. Because the effects of small variations and disturbances in unstable systems are disproportionately large and long-lived, such ESS "remember" those perturbations long after all evidence of the variations and disturbances themselves have disappeared.

While instability and chaos are a sufficient condition for historical contingency, however, they are not necessary. Conditionalities and inheritance are also common forms of path dependence.

So complex nonlinear dynamics (CND) and chaos are useful for analyzing and understanding historically contingent ESS, and are associated with the kind of multiple pathway, multiple outcome thinking necessary to address them. Also, increasingly, CND are more directly linked to concrete empirical observations that underlie the geosciences and in some cases directly to historical sequences or reconstructions. But CND, at least not in any form that I have yet encountered, do not provide an overarching conceptual framework for historically contingent evolution of ESS.

Some of my previous thoughts on dynamical instability & chaos in ESS and their relationship to system evolution:

Phillips, J.D. 1992. Qualitative chaos in geomorphic systems, with an example from wetland response to sea level rise. Journal of Geology 100: 365-374.

Phillips, J.D. 1999. Earth Surface Systems. Complexity, Order, and Scale. Oxford, UK: Basil Blackwell.

Phillips, J.D. 2004.  Divergence, sensitivity, and nonequilibrium in ecosystems.  Geographical Analysis 36: 369-383.

Phillips, J.D.  2006.  Deterministic chaos and historical geomorphology: A review and look forward.  Geomorphology 76: 109-121.

Phillips, J.D., 2017. Soil complexity and pedogenesis. Soil Science 182: 117-127 (or full text preprint here).

Next: Perfection

Posted: 21 July 2017

Evolution (I use the word here in its most general sense of long term historical development) of Earth surface systems is historically contingent and path dependent. This seems to be true of evolution of anything, but I will stick here to my supposed areas of expertise. The state of an Earth surface system (ESS; a landscape, ecosystem, etc.) is a function of generally applicable laws that ultimately determine the range of possibilities, geographically specific place factors (environmental constraints and opportunities), and history. While laws are general, if not universal, and apply to every ESS of a given type (e.g., stream channel, cave, mangrove swamp, soil profile, etc.), the place factors define the template in which those laws operate.

And then there is history.

History includes the initial conditions of ESS development, chains or sequences of events, environmental change, and disturbances of many types. Historical contingency occurs in the form of inheritance (persistence of features or effects from the past), dynamical instability (impacts of changes or disturbances that are disproportionately large and/or long-lasting compared to the disturbance itself), and conditionality. Conditionalities are different trajectories evolution may take according to the occurrence or not of certain events or effects. I have previously called these "Bailey Effects," based on the George Bailey character in the book and movie "It's a Wonderful Life."  The metaphor is explained here, and I note that Stephen J. Gould has used that same story as a metaphor for role of historical contingency in biological evolution.

The patch of land where I sit now, for instance, in its current state is contingent on any number of past climate changes, sea level oscillations, geological events and episodes, biogeographic dispersals, and biological speciations or extinctions (thus, at longer time scales, even the place or geographical factors have elements of historical contingency). On shorter time scales, it depends on tropical storm climatology; the magnitude, timing, severity, and specific tracking of specific tropical cyclones; initial conditions at the outset of these cyclones; and other events and their specifics such as floods, tornadoes, severe rainstorms, and extratropical cyclones. It depends on whether or not lightning strikes or a cigarette is tossed on the ground, whether either ignites a fire, the fuel conditions on the ground and meteorological conditions when a fire ignites, and in the past couple of centuries, whether humans decided to put it out or let it burn. The state of this ESS depends on land ownership and management, and an uncountable number of decisions and happenstances.  Due to teleconnections, the historical contingencies are not even confined to things that happen (or not) here. Climate and sea-level effects of changes in Antarctic ice, sea surface temperatures in the tropical Pacific, and timber prices in India or Brazil may all leave their mark.

And so it is wherever you are right now, and any other place. The details are always different, but the phenomenon of historical contingency is always the same.

So here's what I wrestle with as a geoscientist attempting to understand and interpret ESS evolution: If you look back at a known or hypothesized time zero starting point in terms of what could have happened, or what would happen if you could rewind the clock and start over, there are multiple possible pathways and outcomes at any given point in time. If you think about it in sufficient detail, there may exist infinite possibilities. Note that infinite does not mean that anything could happen--there are an infinite number of even integers for example, but if you choose one at random if cannot be odd or non-integer.

If you represented this as a mathematical directed graph with system states as the nodes and possible changes through time as the links, even if there were just two possibilities at each juncture or point of potential change, there would be 2^q possible states after q episodes of change (storms, lightning strikes, land use decisions, etc.).

However, if you look at the state of an ESS at any given time, the chain of events and state changes that actually led to that would be a linear sequential directed graph--that is, A led to B, B to C, and so on. From this perspective, the observed ESS is a singular outcome of a particular chain of events (constrained by laws and place factors) that could not have turned out any other way. Even if you acknowledge that the hypothetical resetting of the clock or rewinding of the tape would not produce the same result, the fact is that history is irreversible.

So, from the standpoint of an observed or experienced ESS looking back, it is possible that multiple pathways could have led to what you've got, but only one pathway did. It is certain that other trajectories could have led to different outcomes from the same starting point, but only one trajectory and one outcome occurred.

ESS evolutionary sequences. Top: what did happen. Left: what could or could have happened. Bottom right: Typical interpretive situation, with uncertainty about how an observed state did happen, and multiple possibilities.

Looking ahead, multiple future trajectories and outcomes are possible. Those can be constrained based on law and place factors, but the possibilities become larger and essentially limitless further into the future. Yet, of course, only one trajectory will occur, with each change opening up new possibilities but foreclosing other possible pathways.

So what I'm looking for is some sort of mathematical or logical framework or language that can handle these ideas on the one hand, and concrete evidence of actual trajectories on the other--histories, basically. I'm hoping the former can provide a metanarrative to encompass the individual case study stories of the latter.

But I haven't gotten very far. My formal mathematical training was limited to what I had to have to get through college and grad school. I am an enthusiastic, but not particularly talented, autodidact in this regard, but my progress is slow and clumsy. On the geoscience side, I was trained on the process mechanics side of the discipline at time when historical approaches were not only largely ignored, but actively disdained by many.

Those are my excuses for the minimal progress. But in future posts I'll fill you in on what I've been looking at.

Next: Nonlinear dynamics and chaos

Posted: 20 July 2017

The editor of Soil Science, Daniel Gimenez, known for his work on complex nonlinear dynamics and fractals in soils, recently suggested that I write a review paper for the journal updating my ideas on complexity in pedology and pedogenesis. It was an interesting challenge that had not otherwise occurred to me, and I'm glad I did it. The result was recently published as:

Phillips, J.D., 2017. Soil complexity and pedogenesis. Soil Science 182: 117-127 (or full text version here).

The abstract is below:

This paper reviews recent developments in studies of soil complexity, focusing on variability of soil types within soil landscapes. Changes in soil complexity are directly related to divergent and convergent pedogenesis, and in to dynamical stability and chaos. Accordingly, strong links exist between nonlinear dynamical systems theory and studies of soil complexity. Traditional conceptual models of soil formation emphasized convergence of the soil cover in the form of progress toward mature, climax soils. A view of divergence as a frequent occurrence rather than an occasional exception is more recent. Measurement of soil complexity is now firmly linked to field pedology. In addition to strong methodological links to pedometrics and soil geography, standard tools for assessing complexity include chronosequences and other historical approaches, relationships between soil properties and soil forming factors, and pedological indicators. Eight general pathways to changes in soil complexity are identified. Three are based on changes in soil forming factors. These may increase or decrease complexity depending on whether the factors themselves are converging or diverging, and the relative magnitudes of soil and state factor divergence. Three pathways are associated with local disturbances. If these occur less frequently than the relaxation time for soil responses, and if internal pedological dynamics are dynamically stable, then disturbance-induced complexity is reduced over time. Otherwise, divergence and increasing complexity occurs. Two additional pathways are directly related to dynamical stability of intrinsic pedological processes, which may result in decreasing or increasing complexity, either in concert with or independently of environmental controls or disturbances.

Figure 2 (from the paper). Soils formed on Holocene alluvial terrraces in tropical north Queensland, Australia. Divergent pedogenesis associated with preferential flow, differential soil wetting, and accumulation of organic matter and iron oxides is evident. However, it is not known whether these early divergent trends persist or grow over time. The cause-effect or mutual adjustment mechanisms underlying the visually suggested relationships between vegetation tufts and soil properties are also not known.

I just finished reading Paul Bogard's The Ground Beneath Us, (I recommend it), which among other things warns us yet again about the serious issues--environmental, economic, public health, food security--associated with over-reliance on chemical and fossil-fuel intensive industrial agriculture. It's a good 40-years-later follow-up to Wendell Berry's classic Unsettling of America: Culture and Agriculture (Sierra Club Books, 1977).

It also reminded me of a much more technical and difficult book I read a few years back, Jozef Visser's Down to Earth, subtitled "A Historical and Sociological Analysis of the Rise of 'Industrial' Agriculture and the Prospects for the Re-rooting of Agriculture in the Local Farmer and Ecology. Visser, who has graduate degrees in chemistry and a long career in agricultural chemistry, returned to graduate school later in life to produce this book, which is his dissertation from the University of Waginengen (Netherlands). A pdf is available free at the link above, and I recommend it.

Down to Earth has much to say on a complex, multi-faceted topic, but one thing it says that I can't recall seeing anywhere else is that the rise of synthetic nitrogen fertilizer is not only directly linked to the munitions industry, but promoted by collusion between the munitions/agrochemical industry, government, and government-supported scientists.

In the early 20th century a couple of German scientists/engineers developed a method for converting N₂ gas (a form of N not usable by plants or for making explosives) to nitrate and ammonia. It's called the Haber-Bosch process; Fritz Haber and Carl Bosch were later named the most influential chemical engineers of the 20th century. During World War II the industrial capacity for Haber-Bosch-ing skyrocketed to produce explosives. After the war, even though many of the European facilities had been destroyed, the bomb makers had lost the explosives market, and turned their attention to producing NO₃ and NH₄ for synthetic fertilizers. Synthetic N production and artificial (as opposed to organic) fertilizer use skyrocketed.

Even in sources focused mainly on the problems associated with synthetic N, this turn of events is reported as basically a happenstance. In agrochemical-friendly accounts, it is presented as a heroic tale. What Visser shows, however, is that the rise of synthetic N fertilizer involved collusion (conspiracy might not be too strong a word) between the chemical companies, government entities, and some academics supported by the chemical industry and government agencies. And since the U.S. had far more N-making capacity (our factories didn't get blown up in the war), much of this collusion took place in the U.S. (though the German chemical giant BASF, the first to implement the Haber-Bosch process, is also a major player).

You can't really blame the manufacturers for trying to find new markets  (well, you can, but you can't really expect any other behavior). And you can't be too surprised to see government agencies helping to bail out an industry. But Visser makes a strong case that the U.S. Department of Agriculture not only favored research on synthetic fertilizers, but actually suppressed science questioning the need for them or supporting the superiority of organic N.

For all but perhaps the agrochemical industry, it is recognized that agricultural in the U.S. and other industrialized countries has an over-reliance on synthetic N fertilizer, and that in terms of plant nutrition and ecological values, organic N is superior. There is also no real disputing that the overuse of synthetic N is taking a serious toll on natural resources. And, as mentioned above, even the agrochemical industry does not dispute that the manufacture of synthetic N fertilizer evolved from the munitions industry.

What Visser makes clear, and that I wish other scholars would follow up on, is the deliberate collusion between industry and government to make it all happen. It's a lesson even more worth considering in the current environment where heads of U.S. government agencies (Scott Pruitt at EPA being the obvious example) are getting their advice from and having their agendas set by the very entities they are supposed to be overseeing.

Back in 1814, Pierre-Simon Laplace published a classic statement on causal determinism in science. If someone (a hypothetical or metaphorical demon, though Laplace's Demon is apparently a later embellishment; Laplace himself did not use the term) has perfect knowledge of the exact location and momentum of every atom in the universe, their future (and past) values at any time can be perfectly determined from classical mechanics.

One premise of Laplace's Demon is reversibility of physical processes; thermodynamics has refuted that. Other challenges come from quantum mechanics and chaos theory. Though the vision of the 1814 A Philosophical Essay on Probabilities is not widely shared in a strict sense, a more general idea that general laws could predict everything, always, if we only had perfect information persists. And while I have been (and continue to be) active in applications of chaos theory in geosciences, and am convinced of a degree of irreducible uncertainty in environmental phenomena, I agree with the Laplacian worldview in the broader sense. The irreducible uncertainty and indeterminacy that may exist even in non-chaotic systems derives not from a lack of applicable laws (though we certainly have not discovered or fully understood all of those yet), but from the practical impossibility of having perfect information.

Let's take water flows in the terrestrial environment, for example. Though the specifics can get pretty complicated, there are really just four rules governing these flows:

1. Water does not move unless the impelling forces exceed the resisting forces. Thus, for example, if the matric potentials holding water in the soil exceed the gravitational forces pulling it downward, the moisture stays put.

Water staying put in a Minnesota soybean field (photo: Minnesota Crop News).

2. Fluids flow along the most efficient path available. This is roughly comparable to the folk wisdom that water follows the path of least resistance.

3. Concentrated flows are more efficient than diffuse flows. When two water droplets running down the windshield collide, they join into a bigger drop. When two rills join, they stay together as a larger rill, and so on.

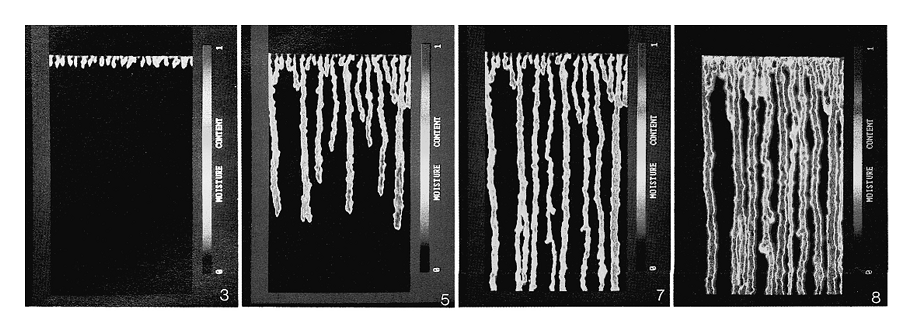"Fingered flow" phenomena (variations in soil moisture content and flow) occur even in apparently homogeneous lab soils due to positive feedbacks and dynamical instabilities (photo: www.geography.hunter.cuny.edu)

4. Water flows toward its base level. This is also reflected in folk wisdom: water seeks its own level. For rivers, for instance, the ocean or an interior basin is the ultimate base level.

All terrestrial water flows and storage patterns are governed by these rules (with their priority reflected in the numerical order). So with only four rules, why are the actual patterns of moisture storage and fluxes in the environment often so complicated, complex, indeterminate, and difficult to predict?

Complex spatial pattern of rills (photo: www.revision.co.zw).

First, of course, there is environmental heterogeneity. The "perfect information" Laplace's Demon would need to have (topography, microtopography, surface conditions, several different soil or substrate properties, vegetation properties, etc.) is both extensive and highly variable. Second, the rules apply on a very local scale. Water cannot "see" the most efficient route to base level, other than in its immediate vicinity--thus each bit of movement is contingent upon the last, and on the immediate surroundings. Third, dynamical instabilities and chaos exist. Small differences matter, and instabilities and chaos indicate that those are amplified, on average.

Agricultural runoff (USDA photo).

Thus hydrology is but one of many examples in the Earth and environmental sciences where the rules may be ratively few and simple, but the outcomes manifold and complex. This may frustrate many scientists sympathetic to some version of the Laplacian vision, but not me. The variable and complex outcomes arising from the simple rules account for the wild and wonderful variety we see in the world around us. Not so much Laplace's Demon, as Laplace's (or this place's) Angel.

Multiple flow paths in an Icelandic landscape (photo: www.Vatnaskii.is).

Karst spring, Kentucky.

Tree uprooting in forests has all sorts of ecological, pedological, and geomorphological impacts. Those are not just related to disturbance--because of the time it takes uprooted trees to decompose, and the distinctive pit-mound topography created, those impacts may last decades to centuries (and sometimes even longer).  One discussion I've often had with colleagues who study this sort of thing has to do with ecosystem engineering and niche construction. Obviously uprooting is a major biogeomorphic process. Obviously it has important impacts on habitat. But do these impacts favor either the engineer species (i.e., the tipped over tree) or some species? Or are they more or less neutral, in the sense of modifying habitat but not necessarily in such a way as to systematically favor any given species?

Uprooted Norway spruce.

Some of my friends and colleagues in the Blue Cats Research Group in the Czech Republic have shown in old-growth forests of central Europe that the mounds eventually resulting from uprooting are favorable sites for new trees to grow, due to favorable soil conditions, and perhaps also freedom from immediately adjacent competition for light, water, etc. (Šebkova et al., 2012).  But sometimes the new tree is the same species as the old one that uprooted, sometimes not (often one cannot tell, but they have awesome historical tree census records at their sites).  The new mound-trees were often European beech, suggesting that the ecosystem engineering effects might be positive or negative, depending on whether the uprooted tree was beech or not. However, we could not dismiss the notion that, since there is a thriving population of beech around, that it could simply be seed source effects--that is, with plenty of beech nuts around in a mature late-successional forest, maybe odds are that any favorable opportunity for new tree growth favors Fagus sylvatica.

Mature Fagus sylvatica on old tree throw mound.

Now comes another study out of central Europe, lead-authored by another friend and colleague (Pawlik et al., 2017) that pretty much nails it down, at least for their sites in Poland's Sudetes Mountains. The short version of the story is that the forest was originally a mature mixed forest, including beech, spruce, and other species. That was replaced, as is often the case in that part of the world, by a Norway spruce-dominated forest in the 19th and early 20th century (spruce is favored by the timber industry). Spruce has a much shallower, spreading root system than beech, and is therefore more prone to uprooting (though Fagus certainly does get uprooted). A windstorm in 1933 caused widespread uprooting in the forest among the Picea abies, with the usual pit and mound microtopography eventually resulting. The mounds (rather than the pits) are overwhelmingly the favorite sites for tree regeneration since, and the new trees are mainly beech. Because beech were few and scattered, this cannot simply be a seed-source phenomenon.

Mature Fagus sylvatica on old tree throw mound.

Thus, at least there, uprooting of Picea constitutes passive ecosystem engineering (i.e., does not necessarily favor the engineer species) and negative niche construction (favoring organisms other than the engineer).  In addition to the effects on uprooting, differences in root architecture also influence interaction with bedrock and thus weathering and moisture flow and other aspects of soil and regolith development  (see review by Pawlik et al., 2016).  Further, beech and spruce litter differs greatly in composition, leading to substantial differences in soil chemistry and microbiology.

Uprooted Norway Spruce, above, and root mound of uprooted beech. Note the difference in thickness. 

Thus, the biogeomorphic effects of uprooting not influence species composition, forest succession, and local soil properties, but the entire (bio)geomorphic regime of a hillslope or forest stand (see, e.g., Phillips et al., 2017).

--------------------------------------------------------------

Note: photos are from my collection, taken in forests in the Czech Republic similar to those discussed above, but are not related to those specific studies and not originally intended to illustrate the phenomena involved.

---------------------------------------------------------------

References:

Pawlik, L., Musielek, L., Migon, P., Wronska-Walach, D., Duszynski, F., Kasprzak, M., 2017. Deciphering the history of forest disturbance and its effects on landforms and soils--lessons from a pit-and-mound locality at Rogowa Kopa, Sudetes, SW Poland. Bulletin of Geography, Physical Geography Series 12, 59-81.

Pawlik, L., Phillips, J.D., Samonil, P., 2016. Roots, rock, and regolith: biomechanical and biochemical weathering by trees and its impact on hillslopes - A critical literature review. Earth-Science Reviews 159: 142-159.

Phillips, J.D., Šamonil, P., Pawlik, L., Trochta, J., Daněk, P., 2017.  Domination of hillslope denudation by tree uprooting in an old-growth forest. Geomorphology 276: 27-36.

Šebkova, B., Šamonil, P., Valterra, M., Adam, D., Janik, D. 2012. Interaction between tree species populations and windthrow dynamics in natural beech-dominated forest, Czech Republic. Forest Ecology and Management 280, 9–19.

The biogeomorphic impacts of organisms may differ at different stages in the development of landforms, ecosystems, or the individual organisms. I was thinking about this recently here along the shoreline bluffs of the Neuse River estuary, North Carolina, where I have been both looking at some soil profiles and enjoying the coastline.

There are at least five distinctly different biogeomorphic roles trees play along this shoreline--many more if you wanted to get more specific within these categories. The specifics are probably of only limited applicability elsewhere, but the general principle--multiple effects, which vary at different stages of both landform and vegetation development--is widely valid.

Trees and other vegetation grow thick and fast in this moist subtropical climate.

Stage 1A Surface Bioprotection

Trees (including canopy, roots, and litter) protect the ground surface from erosion and add organic matter to soil.

This spot where a tree was recently removed shows the local deepening of the soil (compare to sedimentary layering preserved adjacent) associated with a mature tree.

1B Regolith and Soil Formation

Tree roots penetrate substrate, displacing mass and creating local density differences. Moisture is funneled along trunk and roots. CO₂ production by root, rhizosphere, and associated microbial communities facilitate weathering. Organic acids formed by water in contact with roots and litter, facilitating weathering and translocation.

Toppled trees along the Neuse River estuary shoreline.

Stage 2 Bioturbation, Erosion, and Mass Wasting

Cliff/bluff shoreline retreat undermines trees, or exposes them to outward (toward estuary) windthrow. Uprooting removes material from bluff top, reinforcing shoreline retreat.

Toeslope debris--woody and sedimentary.

Waves during high water must remove toeslope debris before undercutting the bluffs.

Stage 3 Shoreline Bioprotection

Toppled trees and large woody debris protect bluffs, absorb wave energy, and trap sediment from both bluff and beach sources. This toeslope sediment and debris must be removed during storms to reinitiate shoreline retreat.

Long term observation of these shorelines shows that tree trunks and woody debris are both added and removed by wave and current processes, as well as added by erosion of adjacent bluffs.

Stage 4 Deposition

Dead trees and woody debris transported and redeposited along shore or at river bottom. Wood may have local effects in deposition or scour, as well as surface roughness.