The Perpetual Quest for Efficiency Part 3: Why Isn’t Everything Always Becoming More Efficient?
The principle of gradient selection, along with a variety of “optimality” principles in geomorphology, geophysics, hydrology, and ecology (e.g., Patten, 1995; Fath et al., 2001; Lapenis, 2002; Ozawa et al., 2003; Kleidon et al., 2010; Quijano and Lin, 2014), is in essence a particular case of a broader principle of efficiency selection. Given this common behavior in many types of Earth surface systems, why do we not observe a general global trend toward ever more efficient routes and networks of flows?
First, note that gradient and efficiency selection are tendencies that (like natural selection in biological evolution) apply in the aggregate, and not to individual cases. Also recall from part 2 that gradient selection is imperfect even where it operates.
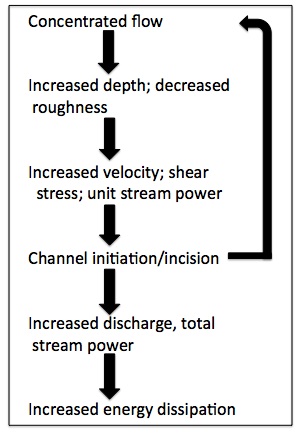
Second, the least action principle means that any work is done using the least amount of energy. That means that any excess energy must be dissipated, and this dissipation may directly (or indirectly via its morphological effects) modify the most efficient flow paths. This is best established for turbulent fluid flows, and has been most clearly illustrated by Nanson and Huang (2016) in their work on least action principles in stream channels.
A third factor mitigating against steady progress toward maximum efficiency is the highly local nature of gradient selection. The wanderer through the brush cannot see the clearing beyond the immediate field of vision, and by choosing the immediate easiest path may miss it entirely. Thus local variations in resistance can result in paths much different from what would occur to achieve maximum efficiency at the broader scale (see, e.g., Hunt’s (2016) discussion of this phenomenon with respect to subsurface fluxes).
This is related to the phenomenon of canalization. The term is used most commonly in its literal sense, with respect to anthropic channelization of river channels or canal construction, or channel incision, and in evolutionary biology. In evolutionary genetics canalization refers to the shaping and constraint of evolutionary pathways by selection (Waddington, 1957). The concept also applies to development of ecosystems and biosphere evolution (Levchenko, 1997). Once local selections are made, in either the evolutionary sense or with respect to flow paths, this constrains or influences future paths.
A fourth barrier to attainment of maximum efficiency is the inherent dynamism of the planet and its environmental systems. Boundary conditions are variable due to climate change, tectonics, sea-level change, and other factors, and ESS are more or less constantly adjusting to those changes. Disturbances also modify or destroy flow paths, both accidentally and deliberately (through anthropic impacts and ecosystem engineering).
Fluviokarst stream, central Kentucky
Finally, we must bear in mind that many different forms of matter and energy are in flux in ESS, and many different entities or phenomena may direct or influence those fluxes. Thus, for example, even though in a fluviokarst system water will always locally prefer the most efficient route, the “competition” between surface fluvial and subsurface karst flow paths can result in either or both of the fluvial and ground water networks being globally suboptimal. Beavers or humans seeking to optimize water storage and flux for their own needs may dam streams and deliberately disrupt the optimal hydrologic flow path. And, there are opportunistic legacy effects—joint and fracture patterns in rock, unrelated to flow dynamics, become preferential pathways for root growth, moisture flux, weathering, and dissolution. Similarly, paths selected by burrowing fauna or roots as most efficient for their needs may not be the most efficient for subsequent water flow, and surface flows utilize inherited valleys or channels created by other geomorphic processes.
Thus the tendencies toward maximum efficiency are often unrealized, or incompletely realized.
References:
Fath BD, Patten BC, Choi JS (2001) Complementarity of ecological goal functions. Journal of Theoretical Biology 208: 493-506.
Hunt AG (2016) Spatio-temporal scaling of vegetation growth and soil formation from percolation theory. Vadose Zone Journal 15: DOI: 10.2136/vzj2015.01.0013.
Kleidon A, Malhi Y, Cox PM (2010) Maximum entropy production in environmental and ecological systems. Philosophical Transactions of the Royal Society B 365: 1297-1302.
Lapenis AG (2002) Directed evolution of the biosphere: biogeochemical selection or Gaia? Professional Geographer 54: 379-391.
Levchenko VF (1999) Evolution of life as improvement of management by energy flows. International Journal of Computing Anticipatory Systems 5: 199-220.
Nanson, G.C., Huang, H.Q., 2016. A philosophy of rivers: equilibrium states, channel evolution, teleomatics and the least action principle. Geomorphology doi:10.1016/j.geomorph.2016.07.024.
Ozawa H, Ohmura A, Lorenz RD, Pujol T (2003) The second law of thermodynamics and the global climate system: a review of the maximum entropy production principle. Reviews of Geophysics 41: 1018, doi:10.1029/2002RG000113.
Patten BC (1995) Network integration of ecological extremal principles: exergy, emergy, power, ascendency, and indirect effects. Ecological Modelling 79: 75-84.
Quijano J, Lin H (2014) Entropy in the critical zone: a comprehensive review. Entropy 16: 3482-3536.
Waddington CH (1957). The Strategy Of The Genes. George Allen & Unwin.