Flows of mass and energy occur along the steepest gradients of potentials or concentrations. The principle of gradient selection is simply that features associated with these gradients persist and grow. Take, for instance, the redistribution of excess (i.e., more than the ground can absorb or retain) surface water. Hydraulic selection principles favor the most efficient paths, which we can generally interpret as the fastest pathways. Thus the steepest slopes and/or the routes with the lowest resistance to flow attract more water. The most efficient paths persist and prevail; less efficient options dry up. For example:
Standard flow resistance equations are of the general form
V = f(RaSbf-c)
where R is hydraulic radius (cross-sectional area divided by wetted perimeter; typically roughly equal to mean depth), S is slope (hydraulic gradient), and f is a roughness or frictional resistance factor. The exponents a, b, c < 1. For example, the D’Arcy Weisbach equation is
V = 8g R0.5 S0.5 f-0.5
Thus flow pathways where water is concentrated (greater R), slope is steeper (greater S) and resistance is lower (smaller f) are favored. Therefore concentrated flows (greater R, lower f) are favored over diffuse flows and steeper paths over gentler gradients.

Gradient selection at work: even in flat topography concentrated flows tend to evolve and dominate (photo: L. Betts, USDA).
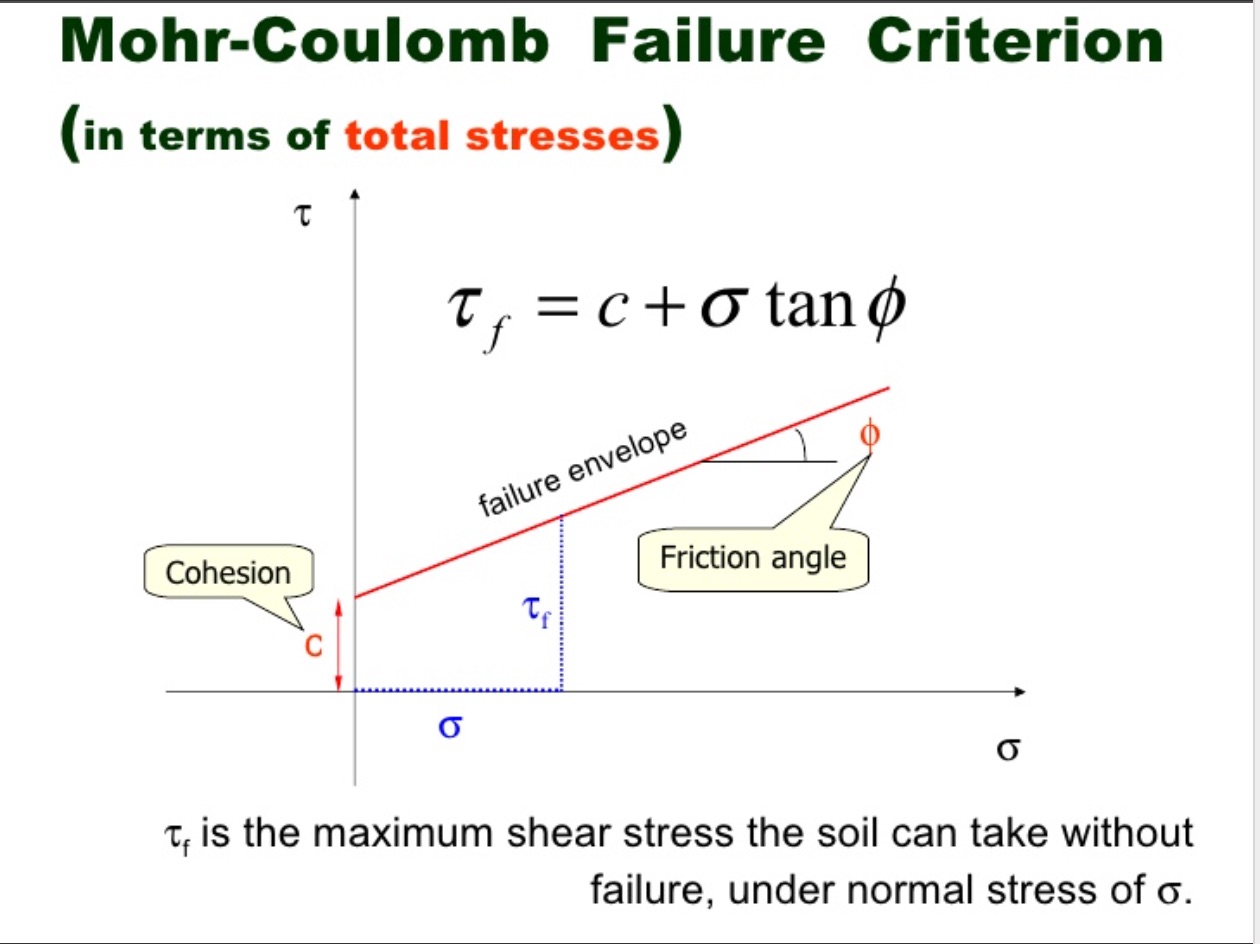
The force or shear stress exerted by a flow against its boundary is given by mean boundary shear stress (tau):
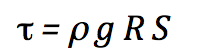
with rho the density of water, and g the gravity constant. With R in m, tau has units of N m-2.

where Acx is the cross-sectional area of flow, and Q = Acx V.
Hydraulic selection favors pathways with faster V, and also deeper R, and steeper S. Thus hydraulic selection also tends to locally maximize shear stress and stream power. This is not a goal function or a basic principle of fluid flows—rather it is an emergent property; a byproduct. There is no principle that runoff and stream flow seek to maximize local shear stress or stream power; rather that is a corollary of hydraulic selection, which in turn expresses ideas we knew from our earliest experiences as children, on a rainy day or playing in a stream—water follows the steepest slope or the path of least resistance.
The emergent local concentration of force and power means that, at least occasionally, force will be sufficient to scour channels. This provides positive feedback reinforcement to hydraulic selection, and channels tend to persist. Steeper, larger, and hydraulically smoother channels are favored over smaller, shallower, rougher, and more gently sloping ones.
I may (or may not) have been the first to describe this as hydraulic selection (a specific form of gradient selection; Phillips, 2010), but I was hardly the first to recognize this as a selection phenomenon. Twidale (2004: 170) characterized channel formation as a process of natural selection, and Nanson and Huang (2008) outlined a principle of “survival of the most stable” with respect to channel configurations.
The "constructal law" of Bejan (2007) expresses basically the same idea as gradient selection: “For a flow system to persist in time (to survive) it must evolve in such a way that it provides easier and easier access to the currents that flow through it." Bejan (2007) provides examples of natural phenomena that illustrate this type of development, including wedge-shaped turbulent shear layers, jets and plumes, the frequency of vortex shedding, B́enard convection in fluids and fluid-saturated porous media, dendritic solidification, and coalescence of solid parcels suspended in a flow.
Michael Woldenberg derived these principles for channelized water flows in 1969 (Woldenberg, 1969). Lin (2010) critically reviewed literature on the prevalence of preferential flow paths of water at a wide range of scales, and the tendency for these to either be controlled by, or to evolve into, morphological features in soils and landscapes. By coupling traditional path-of-least-resistance reasoning to persistence of preferred flow paths, constructal-type behavior emerges, though Lin (2010) pointed out that constructal theory does not address the fact that flow patterns in natural hydrologic and pedologic systems are often strongly influenced by factors other than the flow itself.
Surface water flow is an archetypal example of gradient selection, but numerous other examples exist, including subsurface flows and associated processes. Water moves along paths of least resistance such as rock joints, macropores, faunaul burrows, zones of higher hydraulic conductivity, etc. Weathering, dissolution, erosion, and sediment transport within these features enhances these pathways at the expense of other nearby zones. This can occur even in homogeneous materials due to unstable growth of minor initial variations in moisture content. This results in unstable wetting fronts, fingered flow, and other preferential flow phenomena, which are manifested not only at the event scale, but often influence regolith and landform development (Dekker and Ritsema, 1994; Liu et al., 1994; Phillips et al., 1996; Ritsema et al., 1998; DiCarlo et al., 1999; Lin, 2010). The work of Heckmann and Schwangert (2013) indicates comparable phenomena at work on other hillslope processes, such as landslides and mass wasting.
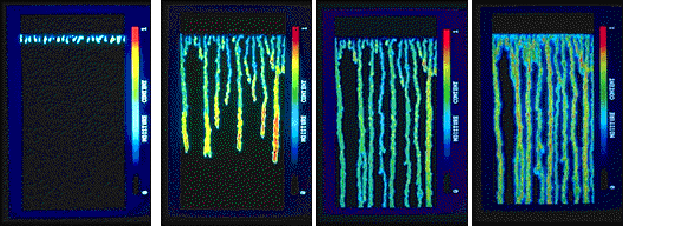
The way water forms fingers in homogeneous sandy soils. Images are produced by passing light through sand and converting the different intensities to different colors (black = low moisture content; red = saturation) (http://soilandwater.bee.cornell.edu/Research/pfweb/educators/intro/fingerflow.htm)
Over time scales several orders of magnitude faster, air flows follow the “topography” described by isobars, which determine pressure gradients. Wind velocities are higher and air movement is greater where pressure gradients are greater, and vice-versa. Positive feedbacks also occur in these phenomena, as observed in the strengthening of high and low pressure systems, but these run their course in a matter of hours or days.
Resistance selection
Gradient selection as described above can be thought of as positive selective processes, dominated by less resistant paths of flow or change, and positive feedback, which reinforces changes associated with evolving flux pathways. Resistance selection, by contrast, is a negative form of selection dominated by resistant or repellent features, resulting in the persistence of more resistant forms or features. The principle of resistance selection simply states that more resistant features (relative to applied forces, or more generally, drivers of change) are selected for preservation, while less resistant components are preferentially lost or modified.
Resistance selection is closely related to, and in some cases simply an inverse way of describing or conceptualizing, gradient selection. Both reflect the effects of variations in the ratio of force (or other drivers of change) to resistance. In some landscapes, however, the resistant residuals--for example karst towers, or the ridgetops in dissected plateaus--rather than the preferred flow paths are the most obvious landscape characteristic. For our purposes, however, resistance selection is considered to be a subset of gradient selection.
Natural selection
The most famous notion of selection in nature is, of course, the principle of biological evolution by means of natural selection, originally articulated by Charles Darwin and Alfred Russel Wallace. Because of this, some object to the use of selection terminology in other scientific contexts. The use of the term “selection” here in gradient and resistance selection is not meant to imply any analogy between mass flux and landscape change phenomena with organisms. In some cases biota are critical components of the latter, and in some instances organic metaphors may be helpful, but please recognize that differences between, e.g., stream channels or soils and organisms in no way invalidates the application of selection concepts to the former. That is, I ask you to concede that use of the word “selection” does not have to be restricted to biological and organic phenomena. In fact, I searched for a different word, but my thesaurus yielded only “choice,” which carries teleological or anthropomorphic baggage we don’t want.
In common with biological natural selection, gradient and resistance selection are emergent properties, arising from tendencies for certain configurations to persist, and for others to decline. I claim no other similarities.
Canalization and contingency
Once gradient or resistance selection has caused a particular configuration or pathway to be favored, positive feedbacks often reinforce it, as described earlier. This in turn often leads to a type of historical contingency called canalization. Once a channel is scoured or a canal constructed, this profoundly effects (and constrains) future water flows. The idea of canalization is that historical contingencies—for example evolutionary pathways, or development of structural relationships—direct future developments. Canalization originally appeared in evolutionary biology with respect to the notion of genetic canalization enhancing stability (Waddington, 1942), but the concept was subsequently broadened.
Levchenko and Starobogatov (1997) discussed canalization with respect to biological evolution. The previous development of biological systems prohibits some trajectories, and preferentially favors others. More specifically, they argue that the biosphere canalizes evolution independently of abiotic factors. Levchenko (1999) provided more detailed examples based on energy flows in evolutionary dynamics. Could this be a more direct link between gradient selection and biological selection?
--------------------------
Bejan, A., 2007. Constructal theory of pattern formation. Hydrology and Earth System Sciences 11, 753–768.
Dekker, L.W., Ritsema, C.J., 1994. Fingered flow: the creator of sand columns in dune and beach sands. Earth Surface Processes and Landforms 19, 153–164.
DiCarlo, D.A., Bauters, T.W.J., Darnault, C.J.G., Steenhuis, T.S., Parlange, J.-Y., 1999. Lateral expansion of preferential flow paths in sands. Water Resources Research 35, 427–434.
Heckmann, T., Schwanghart, W., 2013. Geomorphic coupling and sediment connectivity in an alpine catchment - exploring sediment cascades using graph theory. Geomorphology, 182, 89-103.
Levchenko, V.F., 1999. Evolution of life as improvement of management by energy flows. International Journal of Computing Anticipatory Systems 5, 199-220.
Levchenko, V.F., Starobogatov, Y.I., 1997. Ecological crises as ordinary evolutionary events canalised by the biosphere. International Journal of Computing Anticipatory Systems 1, 105-117.
Lin, H., 2010. Linking principles of soil formation and flow regimes. Journal of Hydrology 393, 3–19.
Liu, Y., Steenhuis, T.S., Parlange, Y.-S., 1994. Formation and persistence of fingered flow fields in coarse grained soils under different moisture contents. Journal of Hydrology 159, 187–195.
Nanson, G.C., Huang, H.Q., 2008. Least action principle, equilibrium states, iterative adjustment and the stability of alluvial channels. Earth Surface Processes and Landforms 33, 923–942.
Phillips, J.D. 2010. The job of the river. Earth Surface Processes and Landforms 35: 305-313.
Phillips, J.D., Perry, D., Carey, K., Garbee, A.R., Stein, D., Morde, M.B., Sheehy, J. 1996. Deterministic uncertainty and complex pedogenesis in some Pleistocene dune soils. Geoderma 73: 147-164.
Ritsema, C.J., Dekker, L.W., Nieber, J.L., Steenhuis, T.S., 1998. Modeling and field evidence of finger formation and finger recurrence in a water repellent sandy soil. Water Resources Research 34, 555–567.
Twidale, C.R., 2004. River patterns and their meaning. Earth-Science Reviews 67, 159–218.
Waddington, C.H., 1942. Canalization of development and the inheritance of acquired characteristics. Nature 150, 563-565.
Woldenberg, M.J., 1969. Spatial order in fluvial systems: Horton's laws derived from mixed hexagonal hierarchies of drainage basin areas. Geological Society of America Bulletin 80, 97–112.


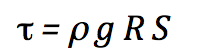


 From Phillips & Lutz, 2008
From Phillips & Lutz, 2008



 (
(