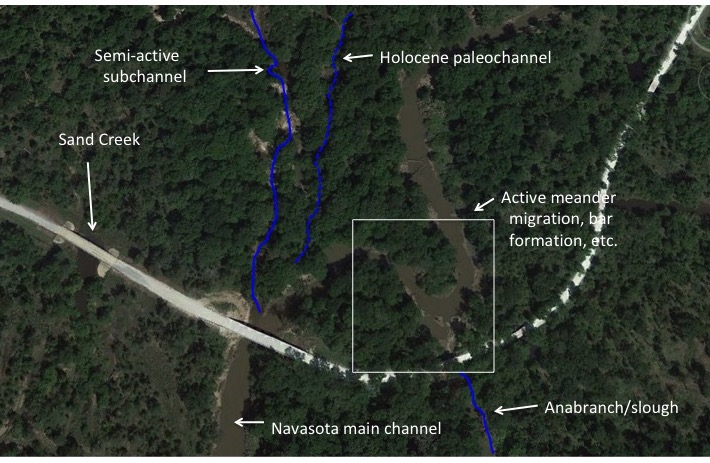
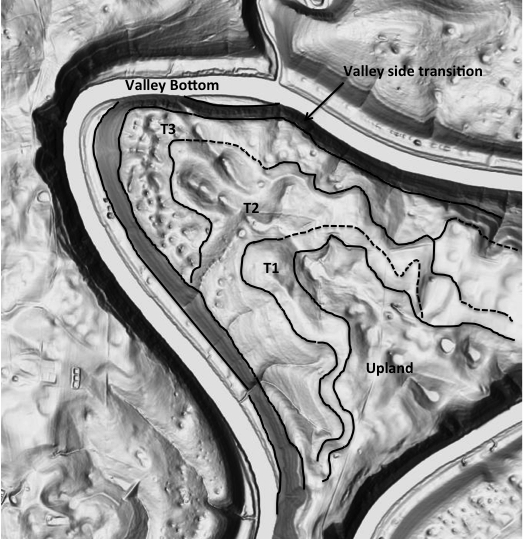
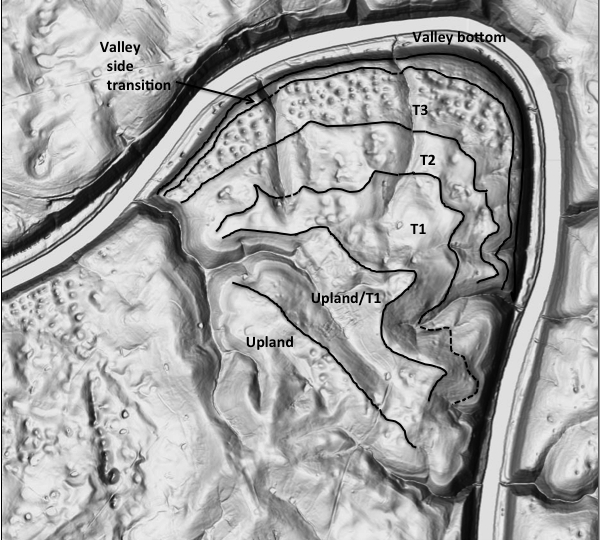
EVOLUTION OF DOLINE DIVERSITY
This post continues a series exploring the idea of evolutionary creativity in Earth Surface systems (ESS). Previous posts introduce the evolutionary creativityconcept, explore the possibility of algorithmic evolution modelsof ESS, and discuss the appearance over time of new varieties of landforms.
-------------------------------------------------------------------------------------------------------
Biologists have put a great deal of effort into identifying the variety of life forms. While there is only one extant species of the genus Homoand 11 of Canis, there are more than 600 species of Quercus (oak trees) and >350,000 of beetles (and counting).