Alluvial rivers are dynamic, and often characterized by lateral migration, formation and eventual abandonment of meander loops, formation of anabranches or distributaries, and relatively abrupt shifts in channel courses. An understanding of river behavior, and effective management of resources in alluvial valleys, requires some understanding of the conditions under which these phenomena occur, and of the relationship between local and broader, reach-scale changes. This can be approached via the concept of dynamical stability.
Stability is often used in geomorphology, hydrology, and engineering in a very general sense to refer to propensity for change and resistance to perturbation. For example, a channel that shows few signs of lateral migration may be considered stable, whereas an actively laterally migrating channel may be characterized as unstable. Dynamical stability has a more rigorous and specific definition. The stability of a dynamical system (such as a river) refers to whether small perturbations tend to be diminished and damped over time, returning the system approximately to its pre-disturbance state. In dynamically unstable systems, effects of small perturbations tend to persist, and to grow disproportionately to the original magnitude of the disturbance. For instance, suppose the disturbance is a levee breach (crevasse) resulting in incision of a new channel across the floodplain. If the new channel relatively quickly infills, restoring the original channel as a single dominant channel, this represents a dynamically stable response, restoring the system to its pre-crevasse state. However, if the new channel persists as an avulsion, forming a new channel course or permanent anabranch, dynamical instability is indicated.

Lower Cape Fear River, N.C. showing multiple channels resulting from avulsions in which both channels persist (Google EarthTM image).

Lower Brazos River near College Station, Texas showing abandoned channels near the modern river resulting from a relocation avulsion (Google EarthTM image).
A tendency exists to categorize geomorphic systems or landforms as a whole as (un)stable. However, dynamical stability is an emergent property, in the sense that stability and instability vary with spatial and temporal scale or with the particular aspect of the system considered. For example, localized instabilities in flow-bed interactions may result in the initiation of bedforms, with resulting broader-scale stability and regularity with respect to bedform size, shape, and spacing. Consider, for example, the difference between the stability of a river reach with respect to flow bifurcations (will the bifurcation persist, or will the new channel degrade or infill?) and the stability of a flow bifurcation itself. The latter concerns whether the split flow configuration is stable, allowing both channels to persist, or unstable, whereby one of the branches will remain or become dominant while the other deteriorates. In this case, dynamical stability of a bifurcated flow is associated with dynamical instability of the reach with respect to avulsions.

An infilling channel along the Sabine River, Louisiana.
With respect to the crevasse case, Slingerland and Smith (1998; 2004) examined the stability of flow bifurcations in the sense of whether a given flow split can persist. Dynamical stability at the scale of flow hydraulics at the bifurcation results in maintenance of the flow split, and thus instability at the broader scale of reach morphology. On the other hand, instability of the flow bifurcation (leading to eventual abandonment of one of the channels) may be related to either dynamical stability or instability at the broader scale, depending on whether the original or the new channel is abandoned. The figure below shows possible local dynamically stable and unstable pathways following a levee breech.
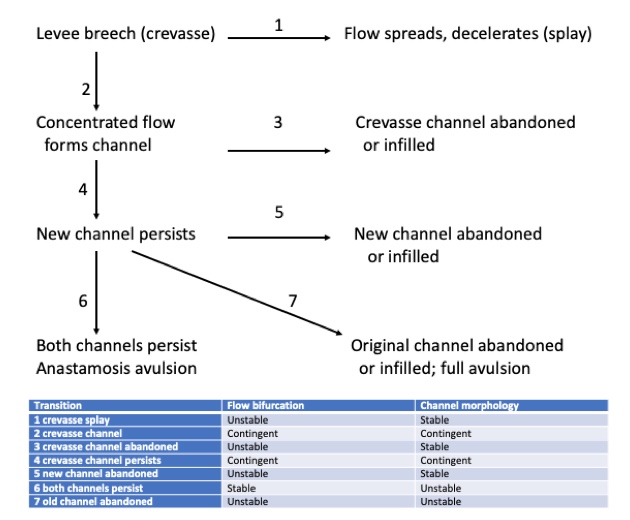
Dynamical stability of flow splits and river channel morphology associated with levee breaches and flow bifurcations. Stable links indicate a return back toward the pre-disturbance state, while unstable paths reflect persistent changes. Contingent indicates that stability is contingent on what happens at subsequent stages.
Many scientists have noted that dynamical (in)stability at different scales may be interconnected—that is, stability at one scale may depend on instability in others. There are, no doubt, many other examples in geomorphology and hydrology.
References
Slingerland, R., Smith, N.D., 1998. Necessary conditions for a meandering-river avulsion. Geology 26, 435–438.
Slingerland, R., Smith, N.D., 2004. River avulsions and their deposits. Annual Review of Earth and Planetary Sciences 32, 257–285.
Questions, comments? Contact jdp@uky.edu
