Geoscientists modeling landscape evolution overwhelmingly (not exclusively, but indeed overwhelmingly) emphasize geophysical aspects, mainly tectonic uplift and erosion. Erosion is typically modeled based on some form of the stream power law, where erosion rates are a power-law function of stream discharge and slope. Discharge is itself often assumed to be a function of drainage area.  There’s nothing wrong with studying the interactions of uplift and denudation without paying much heed to climate, biota, and other factors; I’ve dabbled in this myself.

In a 2009 article, I argued (showed, I like to think) that on a global scale, the biological energy “subsidy” to landscape evolution is comparable to, and even exceeds, the geophysical component. I also introduced a “landscape evolution space” (LES) concept (see also this) attempting to incorporate climatic, biotic, and geophysical contributions. While there is more attention than ever to biotic influences on geomorphology, the LES concept hasn’t gotten much traction, and landscape modeling is still overwhelmingly geophysical. In that’s context, let’s take a look at energy inputs to the Earth’s surface.

The total mechanical power driving global tectonics is 4.8 X 10⁷ watts (W), which translates to 0.297 megajoules (MJ) per square meter per year. By contrast, total solar radiation absorbed the atmosphere and land surface is 240 W m^-2, or 7574 MJ m^-2 yr^-1. On average 5680 MJ m^-2 yr^-1 is absorbed at the surface, and drives biological processes, moisture fluxes, air movements, heat fluxes, etc. (more than 19,000 times the tectonic power). Global mean gross primary productivity (energy used to produce biomass, plus respiration) is estimated at 315 to 420 MJ m^-2 yr^-1.

The mean elevation of the continents is 874 m. Given the density of crustal rocks, the potential energy associated with moving all mass above sea level to below base level averages 22.698 MJ m^-2 . Even if this were entirely accomplished in a century, the rate of potential energy conversion would be only 0.227 MJ m^-2 yr^-1; 2.27 X 10^-5 if we give it a million years, which is still unrealistically fast.

Before any of that mass can be moved, however, it must be converted to transportable material. Estimating the energy required to break down rock is fiendishly difficult, but in the past I’ve used tensile strength (resistance to a force tending to tear a mass apart) as a rough index. Typical tensile strength of rocks ranges from about 4 to 30 megapascals (MPa = 1 MJ m^-3). With a mean of 847 m³ of rock per m² of the land surface, this implies about 3500 to 26,220 MJ m^-2 to get the job done. In the unlikely event it all got done in a century, we’re talking 35 to 262 MJ m^-2 yr^-1. If we give it a million years, then 0.026 to 0.0045 MJ m^-2 yr^-1. Of course, that’s assuming that a cumulative energy input can eventually add up to the threshold tensile strength; we don’t really know if that’s true.

A graphical comparison looks like this:

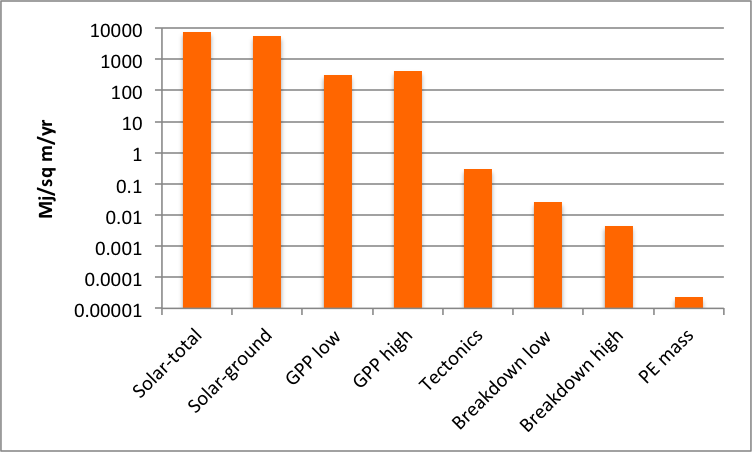
Energy inputs associated with total solar radiation absorption, ground absorption, gross primary productivity, tectonics, rock breakdown, and potential energy (PE) conversion rates associated with reducing continents to sea level. The breakdown and PE figures assume that this is accomplished within 1 Ma, an unrealistically rapid rate.

But wait—the graphic above has a logarithmic scale; otherwise the last four would not be discernible. Below is the same figure with an arithmetic scale, showing that even though the tectonic power is an order of magnitude or more greater than the (unrealistically high) breakdown and PE rates, it is still invisible compared to the solar and biological inputs.

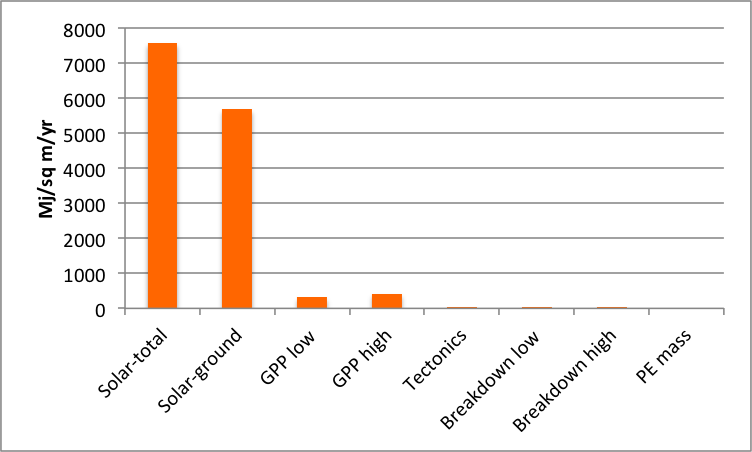
So what does all this mean? First, some caveats—these are rough, back-of-the-envelope calculations based on global estimates of processes that vary wildly geographically and temporally. But still, allowing for error and variability, the implications are pretty clear:

•Solar and biological energy inputs to Earth surface systems are far higher than any energy associated with tectonics or mechanics of mass transfers. Even if only a microscopic fraction of this solar and biological input is geomorphologically significant, it is still a helluva lot!

•Energy inputs required to break down rock  are (at least) two to three orders of magnitude higher than the rate of potential energy conversion associated with moving mass to base-level.

•Energy inputs of tectonic uplift are, globally, more than sufficient to “replenish” losses from denudation.

The basis for the quantitative estimates above comes from:

Phillips, J.D. 2009. Biological energy in landscape evolution.  American Journal of Science  309: 271-290.

Smil, V. 2008. Energy in Nature and Society. MIT Press.